Hi,
How can we explain this Upper bound for the dimension "D" wrt to the size of the data set "n" in knn ? ( why is the 2nd answer true?)
Thanks in Advance!
When we did KNN on lectures we mentioned this lemma:
This lemma states that the loss of KNN classifier is bounded by twice as loss of Bayesian classifier (f*) plus some function that depends on N and D. We want that function to be as small as possible. It holds that:
So, if ln N >> d, than -ln N/(d+1) tends to -infinity. If ln d -ln N/(d+1) also tends to -infinity, than the whole expression will tend to 0, and that is what we want. However, in order to assume that, I think that we need slightly stronger assumption: lnN>>d lnd.
Although it is not a complete answer, I hope this helps a bit
Q3 exam 2017
Hi,
How can we explain this Upper bound for the dimension "D" wrt to the size of the data set "n" in knn ? ( why is the 2nd answer true?)
Thanks in Advance!
When we did KNN on lectures we mentioned this lemma:
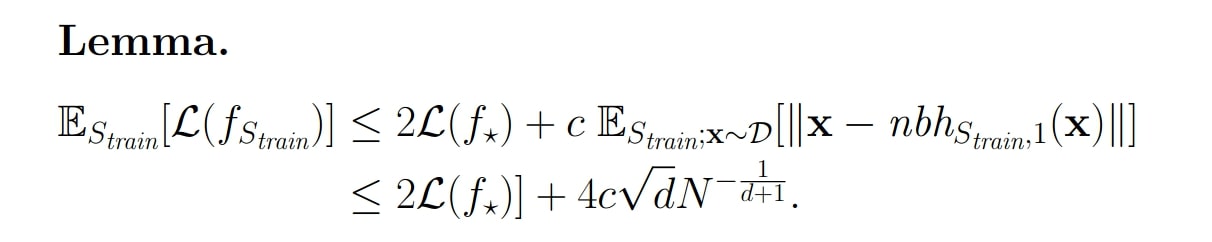
This lemma states that the loss of KNN classifier is bounded by twice as loss of Bayesian classifier (f*) plus some function that depends on N and D. We want that function to be as small as possible. It holds that:
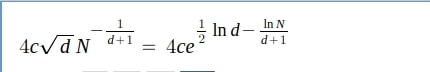
So, if ln N >> d, than -ln N/(d+1) tends to -infinity. If ln d -ln N/(d+1) also tends to -infinity, than the whole expression will tend to 0, and that is what we want. However, in order to assume that, I think that we need slightly stronger assumption: lnN>>d lnd.
Although it is not a complete answer, I hope this helps a bit
Add comment