Let's start from this problem \(\min_{\Vert \delta\Vert_2 \leq \epsilon }y_i w^\top \delta\), to solve this we use the Cauchy-Shwarz inequality to establish a lower bound on the objective that we are minimizing, then show that there is a choice of \(\delta)\) that reaches the established bound, in other words this choice would be a minimizer.
CS gives : \(y_i w^\top \delta \ge -\Vert \delta\Vert_2 \Vert w\Vert_2 \ge -\epsilon \Vert w\Vert_2\), now let's look for a value of \(\delta\) that reaches this lower bound i.e. \(y_i w^\top \delta = -\epsilon \Vert w\Vert_2\) . For this let's start simple and pick \(\delta = \alpha w\) and look for \(\alpha\). Replacing in the equality gives us : \(\alpha y_i \Vert w\Vert_2^2= -\epsilon \Vert w\Vert_2\) , then we find \(\alpha\) and then \(\delta\).
In the general case (for a different norm) we use Holder's inequality in the same spirit as here.
Thank you for your answer,
but regarding what you explained we will then have :
alphay = - epsilon thus alpha = -epsilon/y
and by replacing this alpha in delta=alphaw we'll get:
delta = (-epsilon w )/y with the normalization of w to take into account
So the y factor is at the denominator instead of the numerator, am i wrong or is there a mistake somewhere in the correction?
It goes approximatly in the same way, now you have this problem that you want to solve \(\min_{\Vert \delta\Vert_\infty \leq \epsilon }y_i w^\top \delta\). We use Holder's inequality which say for \(p=1\) and \(q=\infty\) that \(x y^\top \geq - \Vert x\Vert_\infty\Vert y\Vert_1\). So we have : \(y_i w^\top \delta \geq -\Vert \delta\Vert_\infty \Vert w\Vert_1 \geq -\epsilon \Vert w\Vert_1\). Now we look for \(\delta\) that reaches an equality which would be indeed a minimizer. now we want to find \(\delta\) such that \(y_i w^\top \delta = y_i\sum_j \delta_j w_j = -\epsilon \sum_j\vert w_j\vert\) for this it is easy (I hope) to see that it suffices to take \(\delta_j = - y_i \epsilon sign(w_j)\).
Lab10_Pb1_Minimizer Solution
Hello,
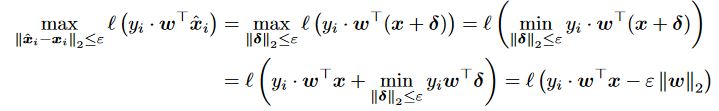
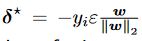
I don't really get how do we find delta* (cf picture) from the equality of the loss we derived:
Thanks!!:)
Let's start from this problem \(\min_{\Vert \delta\Vert_2 \leq \epsilon }y_i w^\top \delta\), to solve this we use the Cauchy-Shwarz inequality to establish a lower bound on the objective that we are minimizing, then show that there is a choice of \(\delta)\) that reaches the established bound, in other words this choice would be a minimizer.
CS gives : \(y_i w^\top \delta \ge -\Vert \delta\Vert_2 \Vert w\Vert_2 \ge -\epsilon \Vert w\Vert_2\), now let's look for a value of \(\delta\) that reaches this lower bound i.e. \(y_i w^\top \delta = -\epsilon \Vert w\Vert_2\) . For this let's start simple and pick \(\delta = \alpha w\) and look for \(\alpha\). Replacing in the equality gives us : \(\alpha y_i \Vert w\Vert_2^2= -\epsilon \Vert w\Vert_2\) , then we find \(\alpha\) and then \(\delta\).
In the general case (for a different norm) we use Holder's inequality in the same spirit as here.
2
Thank you for your answer,
but regarding what you explained we will then have :
alphay = - epsilon thus alpha = -epsilon/y
and by replacing this alpha in delta=alphaw we'll get:
delta = (-epsilon w )/y with the normalization of w to take into account
So the y factor is at the denominator instead of the numerator, am i wrong or is there a mistake somewhere in the correction?
Yes but y is either 1 or -1 so it doesn't matter.
2
Hello,
can you detail also how we obtained delta* for the question 3 with the l_inf norm? (I don't get how we can end up with sign(w))
It goes approximatly in the same way, now you have this problem that you want to solve \(\min_{\Vert \delta\Vert_\infty \leq \epsilon }y_i w^\top \delta\). We use Holder's inequality which say for \(p=1\) and \(q=\infty\) that \(x y^\top \geq - \Vert x\Vert_\infty\Vert y\Vert_1\). So we have :
\(y_i w^\top \delta \geq -\Vert \delta\Vert_\infty \Vert w\Vert_1 \geq -\epsilon \Vert w\Vert_1\). Now we look for \(\delta\) that reaches an equality which would be indeed a minimizer. now we want to find \(\delta\) such that
\(y_i w^\top \delta = y_i\sum_j \delta_j w_j = -\epsilon \sum_j\vert w_j\vert\) for this it is easy (I hope) to see that it suffices to take \(\delta_j = - y_i \epsilon sign(w_j)\).
2
Add comment