I can't seem to understand the calculation done in the first question of the exercise. I understand the idea but I didn't manage to get the correct result. Could you please detail all the steps done in the correction including the derivation of the expression H, the derivative of the regularized loss and the steps regarding the insertion of the SVD expression ? That would help so much to understand
I will try to answer to your last question.
Let's note that H = Q.V.Q^T
w = (H + µ.Id)^-1 H.w
w = (QVQ^T + µ.Id)^-1 QVQ^T.w
w = (QVQ^T + µ.Q.Id.Q^T)^-1 QVQ^T.w (We use that Q.Q^T = Id <=> Q.Id.Q^T = Id)
w = [(Q(V+µ.Id)Q^t)^-1] QVQ^T.w (I just factorize the left parenthesis)
w = [Q(V+µ.Id) Q^T] QVQ^T.w (I use the fact that (ABC)^-1 = C^-1.B^-1.A^-1 and Q^-1 = Q^T)
w = Q(V + µ.Id) V.Q^T.w (I use the fact that Q^T.Q = Id)
I don't know if anyone else had the same confusion that I had, but for the beginning of the exercice I was sure that \(H(w - w^*) \) was signifying the Hessian with respect to \(w - w^*\) . Acutally it is the following product : \(H \times (w - w^*) \). This confused me and I spent hours not being able to do the derivative for the beginning of problem 3 ... Maybe that will help someone else with the same confusion
Lab 9 Problem 3
Hello,
I can't seem to understand the calculation done in the first question of the exercise. I understand the idea but I didn't manage to get the correct result. Could you please detail all the steps done in the correction including the derivation of the expression H, the derivative of the regularized loss and the steps regarding the insertion of the SVD expression ? That would help so much to understand
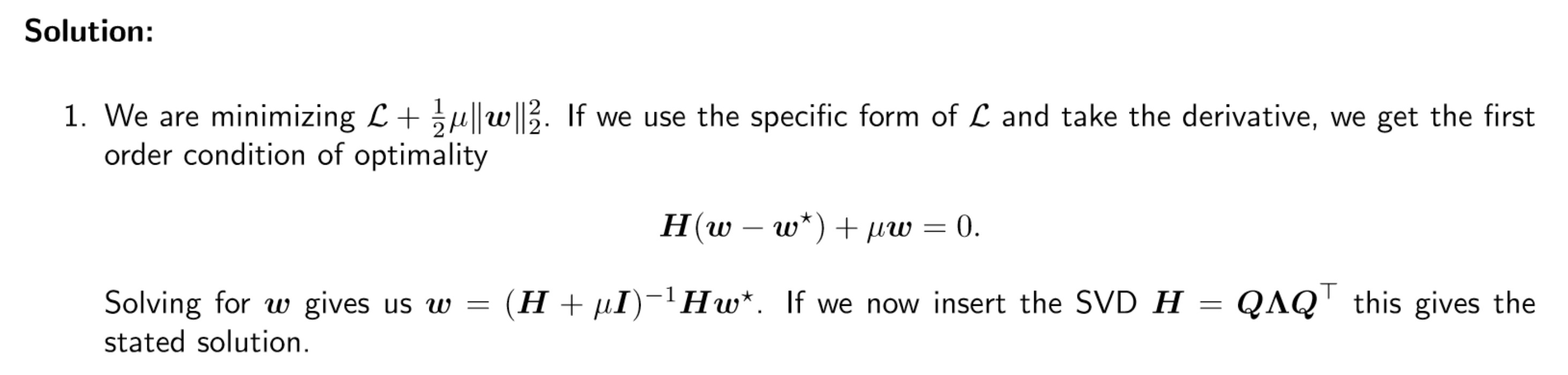
Thank you very much in advance!
1
Hi,
I will try to answer to your last question.
Let's note that H = Q.V.Q^T
w = (H + µ.Id)^-1 H.w
w = (QVQ^T + µ.Id)^-1 QVQ^T.w
w = (QVQ^T + µ.Q.Id.Q^T)^-1 QVQ^T.w (We use that Q.Q^T = Id <=> Q.Id.Q^T = Id)
w = [(Q(V+µ.Id)Q^t)^-1] QVQ^T.w (I just factorize the left parenthesis)
w = [Q(V+µ.Id) Q^T] QVQ^T.w (I use the fact that (ABC)^-1 = C^-1.B^-1.A^-1 and Q^-1 = Q^T)
w = Q(V + µ.Id) V.Q^T.w (I use the fact that Q^T.Q = Id)
Best regards,
Ali
4
Thank you so much! It helps a lot :)
2
I don't know if anyone else had the same confusion that I had, but for the beginning of the exercice I was sure that \(H(w - w^*) \) was signifying the Hessian with respect to \(w - w^*\) . Acutally it is the following product : \(H \times (w - w^*) \). This confused me and I spent hours not being able to do the derivative for the beginning of problem 3 ... Maybe that will help someone else with the same confusion
7
Add comment